重力校正

浩拓软件中的重力校正模块功能是完全按照国家规范标准设计。

常规地面重力校正包含11个功能：

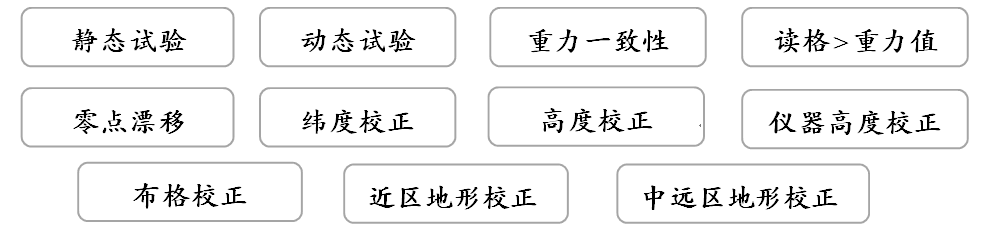
海洋重力校正系列功能是金浩林公司专为海洋勘探定制的专业模块。

海洋版增加8个功能：

重力校正

儒略日转换(Pro)

把从数据采集仪器导出来的儒略日日期转换为常规日期，反之也可以。比如2016年01月23日，转换成儒略日就是2016023，指2016年第23天。儒略日不能直接参与功能运算，需要先通过此功能转换为常规日期格式，然后再参与计算。

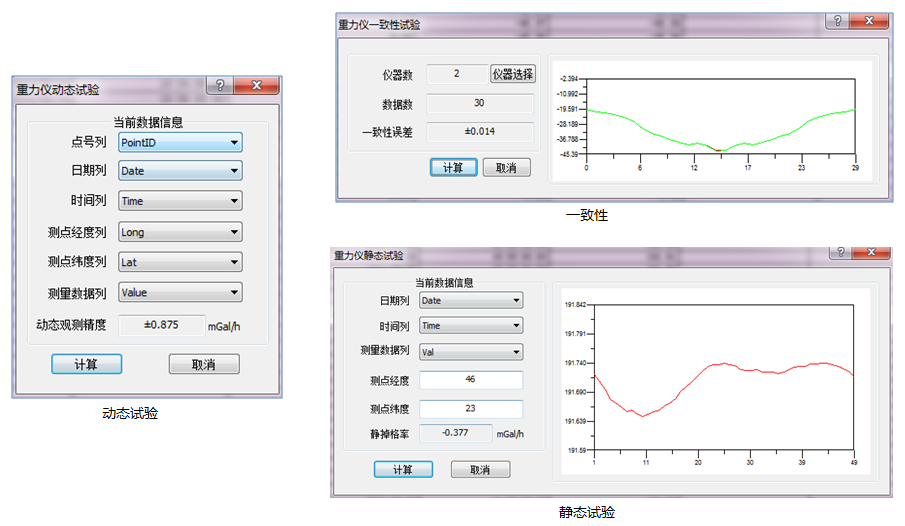
仪器测定

重力勘探中仪器的测定，有仪器的动态、静态和探头一致性的测定，均符合使用标准。

基点比对

通过基点处的绝对重力值把相对重力值换算为绝对重力值，为了减少测量误差的积累，规定数据采集前和采集完成后都要进行基点比对。

固体潮校正

地球在太阳和月亮引力作用下的变形称为地球固体潮。在重力测量中，首先要对重力观测数据进行重力固体潮校正。

参考公式：参考规范 SY/T 6957 – 2013 海洋重力勘探采集技术规程 第8页。

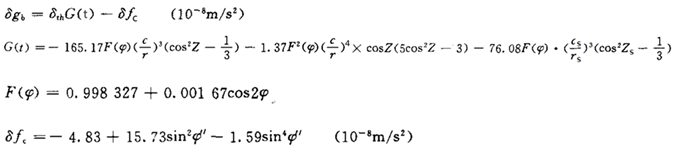
    δ_th——潮汐因子，取1.16； r——月心至地心的距离；c——地心至月心的平均距离；

      r_s——日心至地心的距离；c_s——地心至日心的平均距离；Z_s——太阳对测点的地心天顶距；

      φ——测点纬度；φ′——测点地心纬度；

零点漂移

仪器的零点漂移是时间的函数，严格地说仅指由于弹性元件的疲劳造成读数的变化，亦称为纯零点变化，消除这个读数的变化，就是零点漂移校正。浩拓软件中的零漂算法是参考规范“SY/T 6957 – 2013“ 海洋重力勘探采集技术规程 第9页。

参考公式：

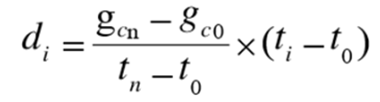
      g_cn和g_c0 —— 晚、早基点读数经格值改正和固体潮改正后的数值。

      t_n和t₀ —— 晚、早基点的读数时间。

吃水改正（Pro）

吃水改正属于海洋校正功能中的海洋校正预处理。

参考公式： 

δg_c=0.3086（hc₁-hc₂）/（t₂-t₁）

δgc —— 吃水改正值，单位为mGal；

hc₁和hc₂ —— 分别是出测前和出测后，测量船左右舷甲板面（重力仪安装位置附近）到水面高度的平均值，单位m，这个值是通过输入实际测量数值来获取；

t₁和t₂ —— 是出海测量前和测量结束后分别同基点进行比对的实际时间，单位h（小时），这个时间通过输入获取。

航迹拟合（Pro）

正交多项式拟合法原理是使得整条测线上的测点坐标与拟合点坐标之间的差值满足加权最小二乘条件，求得正交多项式系数并化为等价的幂多项式形式，用幂多项式将航迹线的坐标表示为时间t的函数，这样就可以根据测线范围内的任意时刻求得对应于该时刻的测线坐标。

                                                                                                拟合前                                                                   拟合后

                                                                                                                              拟合对比效果

厄特沃斯改正（Pro）

由于测量载体和地球相对运动产生的误差，被称为厄特渥斯误差，消除厄特渥斯误差的方法就是厄特渥斯校正。厄特渥斯校正精度主要是由定位精度和测量船的航向和航速精度决定的。在海洋重力测量中，厄特沃什改正一直是影响测量精度的主要误差源。本功能从航迹拟合、合理的航向和航速计算三个方面进行的优化，从整体上提高校正的精度。

参考公式：算法参考规范 SY/T 6957 – 2013 海洋重力勘探采集技术规程 第9页。

δ_ge=7.499×V×sinaA×cosφ＋0.004V²

A—— 航迹真方位角(°)；  V —— 航速 (m/h) ；φ —— 测点地理纬度(°) 。

亦或：

δ_ge=7.50 x[（λ′－λ）÷（t′-t）] x cos²φ

λ′和 λ —— 前测点和后测点的经度(°)； t′和t ——前测点和后测点对应的观测时间( s )；φ —— 当前测点纬度(°)。

测点正常场重力计算

消除测点与基点间由于纬度差异而造成的重力变化，又称为正常场校正。

参考公式：参考规范 SY/T 6957 – 2013 海洋重力勘探采集技术规程 第10页。

    赫尔默特公式：r=978.030(1.0+0.005302Sin²B-0.000007Sin²2B)

    卡西尼公式：r=978.049(1.0+0.005288Sin²B-0.0000059Sin²2B)

    国际地球物理及大地测量联合会公式：r=978.0327(1.0+0.00530244Sin²B-0.00000585Sin²2B)  

     B —— 纬度。

布格校正

布格校正是指在重力测量中，考虑观测点与大地水准面间物质引力影响所做的校正。

布格校正一般由中间层（观测点至大地水准面间存在着假想的无限大的平行岩层）校正和局部地形校正两部分组成。

参考公式：参考规范 DZ/T 0171 – 1997 大比例尺重力勘查规范第19页。

   δ_gB =[0.3086(1+0.0007cos2φ)-0.72×10^-7H- 0.0419ρ×10^-3（1+）-）]×△H

      φ —— 测点纬度；H ——海拔高程，m；△H —— 测点相对于总基点的高差，m；

      ρ —— 中间层密度，kg/m³；R —— 中间层校正半径。

地形校正（包括海洋地形校正Pro）

地形校正是以测点处的平面为标准，消除测点周围高于或低于测点所在平面的物质引力影响，校正后，测点可以看成是处于上面无物质、下面完全被物质充填的无限大的平面上。我国重力地形校正可分为“近区校正”和“中远区校正”两种。

参考公式：“大比例尺重力勘查规范DZ/T 0171-1997”、“区域重力调查规范 DZ/T 0082-93”、“SY/T 6957 – 2013 海洋重力勘探采集技术规程”。

        近区校正三种类型：

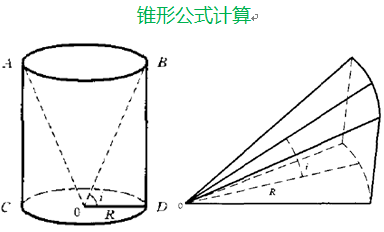
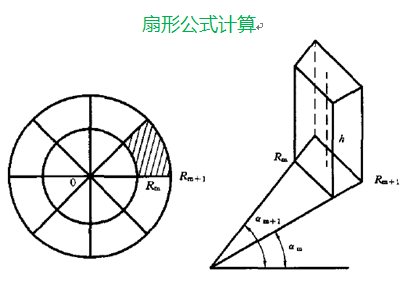
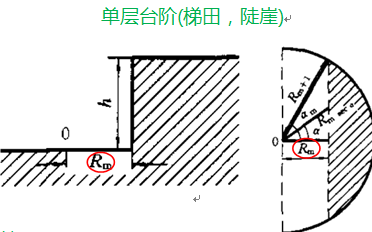
                     锥形（0 - 10 m范围内）                                            扇形（10 - 20 m）                          简单台阶 （如梯田、堤坝类似台阶形）

        中远区校正两种类型：远区地形校正需要配合高精度的地形数据。

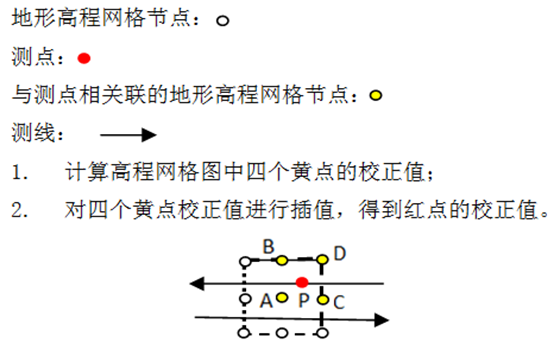
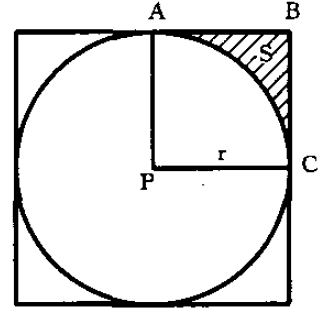
                                                  方域计算方法                                                                                                      圆域图示 

调平（pro）

软件包含“系统调平”和“统计调平”两种方法，能够统计交点差各属性以及均方误差，并且直接能把所有属性生成报告。

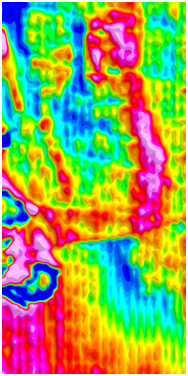
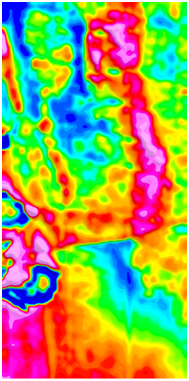
                                            调平前                                                   调平后